gadri: an unofficial commentary from a logical point of view
| This page contains discussions of experimental/scientific/philosophical/logical aspects of Lojban that are non-official and not for everyday usage. You've been warned. |
BPFK's gadri page contains expressions misleading people who have at least a little knowledge of logic (discussion). I (guskant) will make here a commentary on BPFK's gadri so that it is understood by them correctly. (Japanese version/日本語版)
Glossary
We will use the following terms in this commentary.
- argument (sumti)
- Symbol that refers to a referent, or that another argument can be substituted for.
Grammatically, all these are sumti: arguments, {zi'o} which removes a place for an argument, {ko} which refers to listener(s) and forms imperative, {ma} which forms interrogative to ask which sumti makes the statement true, sumti and relative clauses ({zo'e noi broda}...), quantifier and sumti/selbri ({noda}, {ci lo broda}, {ro broda}...) , sumti connected by connectives ({ko'a .e ko'e}...). However, in this article, "sumti" refers to an argument of logic represented in Lojban.
- universe of discourse
- Set of all referents of arguments. It is naturally a universe that is discussed. A universe of discourse depends on the context.
- constant
- Argument that refers to a referent.
- variable
- Argument as a place holder. It does not refer to anything. It is to be substituted for. Variable other than bound variable that will be defined below is called free variable. The truth value of a sentence that includes a free variable is indefinite. Such a sentence is called open sentence.
In Lojban, {ke'a} and {ce'u} are always free variables. A sentence in NOI-clause or NU-clause with {ce'u} is open. (A sentence in NU-clause with no {ce'u} has a truth value, but each of the inside and the outside of NU-clause has an independent universe of discourse, and thus each of them has an independent truth value (for example, see CLL9.7). In definitions of words in Lojban, ko'V/fo'V series {ko'a, ko'e, ...} of selma'o KOhA4 are used as free variables, but it is only a custom for convenience. All cmavo of KOhA2,3,4,5,6 and {zo'e} of KOhA7 are essentially constants. Considering the case that both constants and bound variables (to be defined below) appear in a statement, "constants" are generally considered to be Skolem functions. See Section 3.2.2 for detail.
- quantify
- In substituting possible arguments one by one for a variable in a sentence, count the number of referents that make the sentence true, and prefix the number to the variable.
- quantifier
- Number used for quantification. Besides {pa}, {re}, {vei ny su'i pa (ve'o)} and so on, {ro} "all" and {su'o} "there is one or more" are also quantifiers.
- bound variable
- Variable prefixed by a quantifier. As a result of quantification, there is no room for substituting an arbitrary argument for the variable.
In Lojban, {da}, {de} and {di} are bound variables. For example, {ro da zo'u da broda} means "For all {da} in the universe of discourse, {da broda} is true." In the case that {da}, {de} or {di} are not prefixed by a quantifier, they are regarded as implicitly prefixed by {su'o}.
- domain
- Range of referents to be substituted for a variable, or range to be considered in counting referents in quantification.
In Lojban, a domain of a bound variable can be limited with an expression {da poi...}. For example, {ro da poi ke'a broda zo'u da brode} means "For all {da} that are x1 of {broda} in the universe of discourse, {da brode} is true." If {poi...} does not follow {da}, the domain is the whole universe of discourse.
- tautology
- Sentence that is always true independently of context. {ko'a du ko'a} etc.
- logical axioms
- Sentences selected from tautologies so that all tautologies are proved from them with rules of inference that are defined.
Plural quantification
In order to understand arguments of Lojban from a logical point of view, it is essential to have a knowledge of plural quantification (see, for example, Thomas McKay: Plural Predication, Oxford University Press, 2006).
Plural quantification was invented in order to facilitate expression of proposition that is meaningful only when the referent of an argument is plural.
- Example
- People gathered, cooked and ate.
Logically, this sentence is a proposition that consists of a constant "people" and three predicates "gathered" "cooked" and "ate". The predicates are different from each other in property of treating the argument. We will discuss precisely how the argument in the sentence is treated.
Collectivity and distributivity
Consider the expression "people gathered": based on the meaning of the predicate "gathered", the constant "people" should refer to plural people. When referents of an argument satisfy a predicate as collective plural things like this, we express it as "an argument satisfies an predicate collectively", or "the argument has collectivity".
As for each of the plural people referred to by the constant, each sentence such that "Alice gathered", "Bob gathered" and so on is nonsense. When each referent referred to by a constant cannot satisfy a predicate alone, we express it as "an argument satisfies an predicate non-distributively".
On the other hand, in the expression "people ate", although the constant "people" refers to plural people, the predicate "ate" is satisfied by each person. That is to say, each sentence such that "Alice ate", "Bob ate" and so on is meaningful. When each referent referred to by a constant satisfies a predicate alone, we express it as "an argument satisfies an predicate distributively", or "the argument has distributivity".
Moreover, if the predicate "eat" means an act "put food in a mouth, bite it, let it pass through an esophagus and send it to a stomach", it is hardly considered that "people" satisfies "eat" collectively. Even if a person helps another to eat, the helper is not eater, and the eater is not collective people but an individual. When each referent referred to by a constant cannot satisfy a predicate as collective plural things, we express it as "an argument satisfies an predicate non-collectively". (However, it is possible to interpret the predicate "eat" as involving collectivity. For example, if it is interpreted as "put food away from outside to inside of body", we may say "collectively eat" to express an event that people eat and consume a mass of food together.)
There are also predicates that allow both properties "collectivity" and "distributivity". "People cooked" may mean that plural people knead paste of pizza together, and that each of them is in charge of cakes or pot-au-feu. In this case, the constant "people" refers to plural people, and they cooked pizza collectively, cakes and pot-au-feu distributively. The constant "people" thus satisfies the predicate "cooked" collectively and distributively.
Note that the constant "people" refers to what is common to three predicates "gathered", "cooked" and "ate". No matter if a constant satisfies predicates collectively or distributively, the referent is the same.
If we use an argument "a set of people" in the case of satisfying a predicate collectively, it might be possible to interpret the predicate "gathered" so that the argument satisfies it, but the same argument cannot satisfy the predicate "ate", because we can hardly say that a set of people, which is an abstract entity, performs "ate".
Using plural constants and plural variables that will be discussed in the following sections, we can express plural things in the form of predicate logic without using sets.
Plural constant and plural variable
An argument that refers to referent without introducing a notion of sets, without distinguishing collectivity and distributivity, without distinguishing plurality and singularity, is called plural constant. A variable for which a plural constant can be substituted is called plural variable. Quantifying a plural variable is called plural quantification. A quantifier used for plural quantification is called plural quantifier. A plural variable prefixed with a plural quantifier is called a bound plural variable.
me and jo'u
We introduce relations between plural constants and plural variables: {me} and {jo'u}.
| X me Y (me'u) | X is among Y | |
X and Y represent here plural constants or plural variables. A cluster {me Y (me'u)} is a selbri in Lojban grammar. {me'u} is an elidable terminator of structure beginning with {me}.
{me} has the following properties with arbitrary arguments X, Y and Z:
- X me X (reflexivity)
- X me Y ijebo Y me Z inaja X me Z (transitivity)
- X me Y ijebo Y me X ijo X du Y (identity)
The property 3 means that the identity between referents of X and Y is represented with {me}, as a relation that {X me Y ijebo Y me X}.
| X jo'u Y | X and Y | |
{jo'u} combines two arguments X and Y into one plural constant or one plural variable.
{jo'u} has the following properties with arbitrary arguments X and Y:
- X me X jo'u Y
- X jo'u Y du Y jo'u X
- X jo'u X du X
The property 2 means that the referent of the whole argument does not vary when two arguments combined by {jo'u} are interchanged with each other. The property 3 means that {jo'u} does not add any referent when it combines an argument with itself.
Using {jo'u}, the following expression is possible:
- Example
- B and C gathered, cooked and ate.
- by jo'u cy jmaji gi'e jukpa gi'e citka
Each of {by} and {cy} is a plural constant.
The predicate {jukpa} (cook) can be interpreted collectively and/or distributively, but the plural constant {by jo'u cy} says nothing about whether it satisfies {jukpa} collectively and/or distributively. If we want to make explicit that they cooked "collectively", we say {by joi cy} using {joi} that will be discussed in Section 3.4, or {lu'o by jo'u cy} using {lu'o} that will be discussed in Section 3.3. Contrastively, if we want to make explicit that they cooked "distributively", we say {lu'a by jo'u cy} using {lu'a} that will be discussed in Section 3.3. However, these arguments that says explicitly collectivity and/or distributivity are not always commonly used for other predicates like {jmaji} or {citka}.
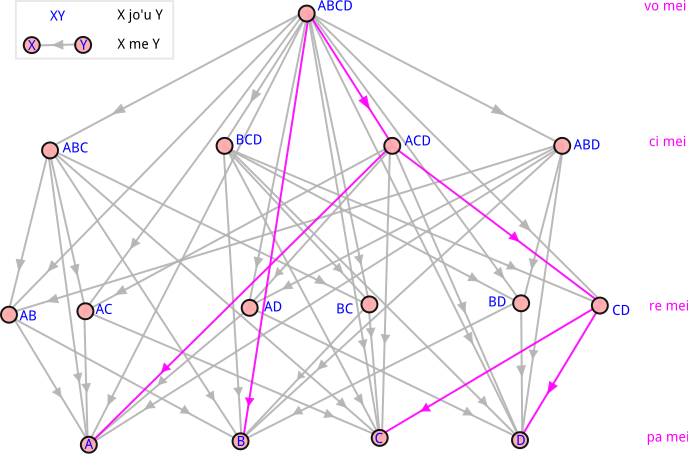
The diagram below shows relations constructed with {me} and {jo'u} represented with a directed graph, in which the vertices represent plural constants.
Individual
Referent of a plural constant is not necessarily plural: a plural constant can refer to one individual. An individual is defined as follows:
| X is an individual | =ca'e | ro'oi da poi ke'a me X zo'u X me da |
where ro'oi is an experimental cmavo proposed by la xorxes, which is a plural quantifier meaning "all". {ro'oi da} is a bound plural variable meaning "for all that can be substituted for {da}". This definition means that X is called an individual when the condition "for all {da} that are among X, X is among {da}" is satisfied. In other words, "in the universe of discourse, nothing other than {X} can be substituted for {da} such that {X me da}" is expressed by "X is an individual".
When each of X and Y is an individual and X is not equal to Y, {X jo'u Y} is called individuals. When each of X and Y is an individual or individuals, {X jo'u Y} is called individuals as well.
Difference between plural and singular
A plural constant that refers to a single individual is called a singular constant.
Unless X=Y and X is an individual, no matter whether each of X and Y is plural or singular, {X jo'u Y} is not a singular constant. It is because
X me X jo'u Y ijenai X jo'u Y me X
holds true, and then {X jo'u Y} does not satisfy the condition of an individual {ro'oi da poi ke'a me X jo'u Y zo'u X jo'u Y me da}.
Bound singular variable
When the domain of a bound plural variable is restricted to what is an individual, the variable is called bound singular variable. A bound singular variable cannot take more than one individual value at a time. {ro da} (for all {da}) and {su'o da} (there is at least one {da}), which are officially defined in Lojban, are bound singular variables. They can be defined with bound plural variables as follows:
| ro da | ro'oi da poi ro'oi de poi de me da zo'u da me de | |
| su'o da | su'oi da poi ro'oi de poi de me da zo'u da me de | |
su'oi is an experimental cmavo proposed by la xorxes, and is a plural quantifier meaning "there is/are". Note that {su'oi} is not "at least one". {su'oi da} is a bound plural variable meaning "there is/are {da}".
What is neither an individual nor individuals
Referent of a plural constant is not necessarily an individual or individuals. It is possible to discuss a universe of discourse such that referent of a plural constant is neither an individual nor individuals.
For example, consider such a universe of discourse in which the following proposition holds true.
ro'oi da poi ke'a me ko'a ku'o su'oi de zo'u de me da ijenai da me de — Condition_1
In other words, in this universe of discourse, for all X such that {X me ko'a}, there is always Y such that {Y me X} and not {X me Y}.
- Theorem
- In a universe of discourse where Condition_1 is true, {ko'a} is neither an individual nor individuals.
- Proof
- Suppose {ko'a} is an individual. From the definition of "an individual":
ro'oi da poi ke'a me ko'a zo'u ko'a me da — Supposition_2
Replace {ro'oi da} with {naku su'oi da naku}:
naku su'oi da poi ke'a me ko'a ku'o naku zo'u ko'a me da — Supposition_2-1
Move the inner-most {naku} into the proposition:
naku su'oi da poi ke'a me ko'a zo'u naku ko'a me da — Supposition_2-2
Replace {su'oi da poi} with {ije} and move into the proposition:
naku su'oi da zo'u da me ko'a ije naku ko'a me da — Supposition_2-3
Replace {ije naku} with {ijenai}:
naku su'oi da zo'u da me ko'a ijenai ko'a me da — Supposition_2-4
By the way, from a property of {me},
ko'a me ko'a
is always true. {ko'a} is therefore in the domain of {da} of Condition_1. Replace {ro'oi da} of Condition_1 with {ko'a}, and it thus holds true:
su'oi de zo'u de me ko'a ijenai ko'a me de — Condition_1-1
Condition_1-1 and Supposition_2-4 contradict each other. Supposition_2 is thus rejected by reductio ad absurdum. It means that {ko'a} is not an individual.
Moreover, when {ko'a} is expanded to {A jo'u B}, from a property of {jo'u}, the following propositions hold true:
A me ko'a
B me ko'a
Each of A and B is in the domain of {da} of Condition_1. Considering similarly to Condition_1-1, neither A nor B is an individual. {ko'a} is thus not individuals. Q.E.D.
When {ko'a} is neither an individual nor individuals, what actually does it refer to? We may interpret that it refers to what is referred to by a material noun, for example. By a speaker who thinks that a cut-off piece of bread is also bread, bread is regarded as neither an individual nor individuals.
(I wrote the same proof only in Lojban.)
A logical axiom on plural constant
The following logical axiom is given to an arbitrary plural constant C:
ganai C broda gi su'oi da zo'u da broda
It means "in a universe of discourse, if a proposition in which a plural constant is x1 of {broda} holds true, there is referent that is x1 of {broda}".
That is to say, an argument that has no referent in a universe of discourse cannot be represented by a plural constant. An argument that has no referent is expressed in the form {naku su'oi da}, which is a negation of a bound plural variable {su'oi da} meaning "there is/are".
Definition of gadri
- lo (LE)
- It is prefixed to selbri, and forms a plural constant that refers to what satisfies x1, the first place of the selbri. If a quantifier follows {lo}, the quantifier represents the count of all the referents of the plural constant. In the case that a quantifier follows {lo}, a sumti may follow it. In this case, it forms a plural constant that refers to what is/are among sumti.
| lo [PA] broda (ku) | zo'e noi ke'a broda [gi'e zilkancu li PA lo broda] (ku'o) | what is/are broda [that is/are PA in total] |
| lo PA sumti (ku) | lo PA me sumti (me'u) (ku) | what is/are among sumti, and PA in total |
{ku}, {ku'o}, {me'u} are elidable terminators.
Putting a quantifier after gadri like {lo PA} is called inner quantification, and the quantifier is called inner quantifier. Although the term "quantify" is involved, it is different from quantification of logic. Inner quantification does not involve counting referents of constants that can be substituted for a variable, but counting all the referents of one plural constant. Inner quantification will be discussed more precisely in Section 3.1.
On the other hand, putting a quantifier before gadri, or before a sumti more generally, is called outer quantification, and the quantifier is called outer quantifier. Outer quantification will be discussed more precisely in Section 3.2.
All sumti formed with gadri are defined so that they are expanded into expressions with {zo'e}. That is to say, the most general plural constant is represented by a single {zo'e}. A sumti formed with gadri is {zo'e} accompanied by an explanation.
- Example
- People gathered, cooked and ate.
- lo prenu cu jmaji gi'e jukpa gi'e citka
While the predicate {jukpa} (cook) can be interpreted collectively as well as distributively, the plural constant {lo prenu} (people) does not say explicitly if it satisfies {jukpa} collectively or distributively. If we want to say explicitly that they "collectively" cooked, we use {loi}, which will be discussed later, and say {loi prenu}. Contrastively, if we want to say explicitly that they "distributively" cooked, we say {ro lo prenu} with an outer quantification, or {lu'a lo prenu}. However, a sumti that says explicitly collectivity or distributivity is not necessarily able to be shared with other predicate like {jmaji} or {citka}.
- le (LE)
- {le broda} refers specifically to a referent of {lo broda}, and explicitly express that the speaker has the referent in mind. Its logical property is the same as that of {lo}.
| le [PA] broda (ku) | zo'e noi mi ke'a do skicu lo ka ce'u broda [gi'e zilkancu li PA lo broda] (ku'o) | |
| le PA sumti (ku) | le PA me sumti (me'u) (ku) | |
- la (LA)
- It is prefixed to selbri or cmevla, and forms a plural constant that refers to what is named the selbri or cmevla string. Its logical property is the same as that of {lo}.
| la [PA] broda (ku) | zo'e noi lu [PA] broda li'u cmene ke'a mi (ku'o) | |
| la PA sumti (ku) | zo'e noi lu PA sumti li'u cmene ke'a mi (ku'o) | |
- loi (LE), lei (LE), lai (LA)
- {loi/lei/lai broda} refers to a referent of {lo/le/la broda}, and explicitly express that the referent satisfies a predicate collectively.
| loi [PA] broda | lo gunma be lo [PA] broda | |
| lei [PA] broda | lo gunma be le [PA] broda | |
| lai [PA] broda | lo gunma be la [PA] broda | |
| loi PA sumti | lo gunma be lo PA sumti | |
| lei PA sumti | lo gunma be le PA sumti | |
| lai PA sumti | lo gunma be la PA sumti | |
Because {loi/lei/lai} is thus defined by another plural constant {lo gunma be lo/le/la}, it does not refer directly to referent of {lo broda} or {lo PA sumti}, but referent of {lo gunma}. Therefore, even if {lo broda} or {lo PA sumti} is not an individual, {loi broda} or {loi PAsumti} can be an individual {lo gunma} under the following condition:
ro'oi da poi ke'a me lo gunma be lo/le/la [PA] broda zo'u lo gunma be lo/le/la [PA] broda cu me da
ro'oi da poi ke'a me lo gunma be lo/le/la PA sumti zo'u lo gunma be lo/le/la PA sumti cu me da
- lo'i (LE), le'i (LE), la'i (LA)
- {lo'i/le'i/la'i broda} refers to a set or sets of individual(s) that constitute(s) a plural constant {lo/le/la broda}. Because {lo'i/le'i/la'i} forms a set or sets, it is defined only when its/their member(s) {lo/le/la broda} is/are an individual or individuals. A set itself is always an individual, and sets are always individuals: there is no set that is not an individual.
| lo'i [PA] broda | lo selcmi be lo [PA] broda | |
| le'i [PA] broda | lo selcmi be le [PA] broda | |
| la'i [PA] broda | lo selcmi be la [PA] broda | |
| lo'i PA sumti | lo selcmi be lo PA sumti | |
| le'i PA sumti | lo selcmi be le PA sumti | |
| la'i PA sumti | lo selcmi be la PA sumti | |
Because {lo'i/le'i/la'i} is defined by another plural constant {lo selcmi be lo/le/la}, it does not refer directly to referent of {lo broda} or {lo PA sumti}, but referent of {lo selcmi}.
In set theory, an empty set is defined as {lo selcmi be no da}, and an expression {lo no broda} is officially meaningless (see Section 3.1. This implies that an empty set cannot be expressed with {lo'i/le'i/la'i}.
According to jbovlaste, {selcmi} is defined as follows:
| x1 selcmi x2 | =ca'e | x1 se cmima ro lo me x2 me'u e no lo na me x2 |
If we accept this definition, a set referred to by {lo'i/le'i/la'i}-sumti consists of only the referent of {lo/le/la [PA] broda} or {lo/le/la PAsumti}. Contrastively, if we define it as {selcmi}={se cmima}, the set may include what is/are other than the referent of {lo/le/la [PA] broda} or {lo/le/la PA sumti}. It is not yet officially determined which interpretation is to be accepted.
Inner quantification
BPFK defines inner quantification as follows:
| lo [PA] broda | zo'e noi ke'a broda [gi'e zilkancu li PA lo broda] | |
| lo PA sumti | lo PA me sumti | |
That is to say, inner quantifier means number of referent counted by unit {lo broda} or {lo me sumti} that is x3 of {zilkancu}. However, instead of {zilkancu}, the meaning of which is too vague for definition, an idea of redefinition using {mei} was suggested as follows:
- Axiom 1
- ro'oi da su'o pa mei
- Definition
| (D1) ko'a su'o N mei | =ca'e | su'oi da poi me ko'a ku'o su'oi de poi me ko'a zo'u ge da su'o N-1 mei ginai de me da |
| (D2) ko'a N mei | =ca'e | ko'a su'o N mei gi'e nai su'o N+1 mei |
| (D3) lo PA broda | =ca'e | zo'e noi ke'a PA mei gi'e broda |
Using these definitions and Axiom 1, the following theorem will be proved.
If and only if {ko'a pa mei}, {ko'a} is an individual.
- Proof
- (D2) is
| ko'a N mei | = | ko'a su'o N mei gi'e nai su'o N+1 mei |
| = | ge ko'a su'o N mei -----(S1) | |
| gi naku ko'a su'o N+1 mei -----(S2) | ||
Applying (D1) to (S2),
| (S2) | = | naku su'oi da poi me ko'a ku'o su'oi de poi me ko'a zo'u |
| ge da su'o N mei | ||
| ginai de me da | ||
| = | ro'oi da poi me ko'a ku'o ro'oi de poi me ko'a zo'u | |
| naku ge da su'o N mei | ||
| gi naku de me da | ||
| = | ro'oi da poi me ko'a ku'o ro'oi de poi me ko'a zo'u | |
| ganai da su'o N mei | ||
| gi de me da | ||
(D2) is therefore
| ko'a N mei | = | ge (S1) gi (S2) |
| = | ge ko'a su'o N mei | |
| gi ro'oi da poi me ko'a ku'o ro'oi de poi me ko'a zo'u | ||
| ganai da su'o N mei | ||
| gi de me da | ||
When N=1,
| ko'a pa mei | = | ge ko'a su'o pa mei |
| gi ro'oi da poi me ko'a ku'o ro'oi de poi me ko'a zo'u | ||
| ganai da su'o pa mei | ||
| gi de me da | ||
Because of Axiom 1, it implies
| ko'a pa mei | = | ro'oi da poi me ko'a ku'o ro'oi de poi me ko'a zo'u de me da |
The right side implies {ro'oi da poi ke'a me ko'a zo'u ko'a me da}, which is the condition for "{ko'a} is an individual". Its converse is also true. Q.E.D.
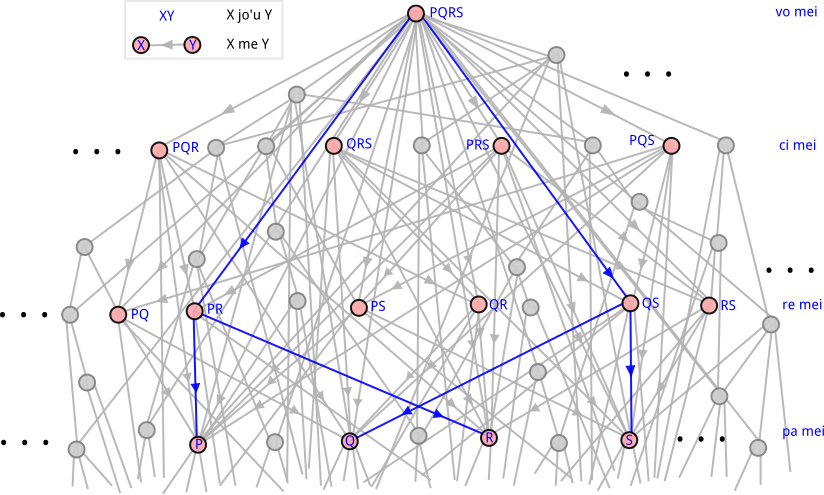
The diagram below shows a procedure of counting something up to four represented with a directed graph. In this diagram, loops such as {X me X} are omitted for simplicity, though they exist. Counting up corresponds to selecting a subgraph of a directed graph formed with {me}: the subgraph that has a form of tree that includes all leaves (constants each of which is an individual) to be counted, for example the part of magenta color in the diagram.
Repeating inner quantification
Because {lo PA sumti} is defined, we can repeat inner quantification to form an argument.
- Example
- lo mulno kardygri cu gunma lo vo loi paci karda A full deck consists of four groups of thirteen cards.
- su'o da zo'u loi re lo'i ro mokca noi sepli py noi mokca ku'o da cu relcuktai Two sets of points that are equidistant from a point P is a double circle.
Problems on inner quantification
Cannot say zero
Because an argument formed by gadri is a plural constant, {lo broda} implies {su'oi da zo'u da broda} according to the logical axiom on plural constant shown in Section 2.2.6. That is to say, the expression {lo no broda} implies "there are what are broda, which are counted 0", which seems meaningless.
This means that official Lojban cannot express negation of existence of plural variable {naku su'oi da}, which is nevertheless necessary, for example in the following situation:
lo xo prenu cu jmaji gi'e jukpa gi'e citka — no
"How many people gathered, cooked and ate?" "zero."
This response is an abbreviated form of {lo no prenu cu jmaji gi'e jukpa gi'e citka}.
This proposition means that {lo no prenu} satisfies selbri {jmaji} collectively and (je) non-distributively, {jukpa} collectively or (ja) distributively, {citka} non-collectively and (je) distributively. Because it includes selbri {jmaji} to be satisfied non-distributively, the sumti cannot be replaced by negation of existence of bound singular variable {naku su'o da}={no da}. Moreover, because it includes selbri {citka} to be satisfied non-collectively, {lo} of the sumti cannot be replaced by {loi}={lo gunma be lo}.
For making such a proposition meaningful, it is essential to give an expression {lo no broda} a meaning of negation of existence of plural variable. For this purpose, I suggest the following definition valid in the case that PA=0 for {lo PA broda}.
- Unofficial definition of {lo no broda}
| lo no broda | =ca'e | naku su'oi da poi ke'a broda |
(If it were defined as {naku lo broda}, the negation would have spanned the whole proposition, and it would not have implied quantification. I abandoned therefore such a definition.)
Cannot quantify material noun or something
Axiom 1 of Section 3.1 excludes sumti that is neither an individual nor individuals from expressions {(su'o) N mei} and {lo N broda}.
Can we use {piPA} for sumti that is neither an individual nor individuals, then? No. Actually, piPA is defined only for outer quantification.
| piPA sumti | lo piPA si'e be pa me sumti | |
As we can see in the definition, the body of outer quantification by {piPA} is plural constant {lo piPA si'e}, which is not a bound singular variable. However, x2 of {piPA si'e} is {pa me sumti}, to which the definition of PA broda is applied:
| PA broda | PA da poi broda | |
As a result, {piPA sumti} is defined only when there is an individual that satisfies x1 of {me sumti}. That is to say, what is neither an individual nor individuals is excluded also from an expression of outer quantification with {piPA}.
What would be if {piPA} were defined also for inner quantification? In that case, the following definition would be desirable to conform the definition of {piPA} of outer quantification:
- Unofficial definition of {piPA} of inner quantification
| lo piPA broda | =ca'e | zo'e noi ke'a piPA si'e be lo pa broda |
This definition of {piPA} of inner quantification still excludes what is neither an individual nor individuals unless {lo pa broda} is defined in another way so that it can be what is neither an individual nor individuals.
Why don't we use {PA si'e} to express quantification of what is neither an individual nor individuals? It is possible, but BPFK's current definition of {si'e} depends on {pagbu}:
| x1 number si'e x2 | x1 pagbu x2 gi'e klani li number lo se gradu be x2 | |
If we interpret {pagbu} so that x1 is not larger than x2 (and this is ordinary interpretation), {si'e} is very inconvenient because the unit should be changed every time counting up. If {si'e} were defined so that PA of {PA si'e} could be larger than 1, {si'e} would have been pragmatic for quantification of what is neither an individual nor individuals.
Besides those considerations, if we abandon Axiom 1 of Section 3.1, Definitions (D1) (D2) (D3) can be applied to what is neither an individual nor individuals. In this case, a speaker should select some plural constants {ko'a, ko'e, ...}, and decide that {[ko'a/ko'e/...] su'o pa mei}; the selection must be done attentively so that referents of plural constants that are {pa mei} do not overlap with each other. Those preparations of {ko'a, ko'e, ...} and (D2) imply only
| ganai [ko'a/ko'e/...] pa mei | ||
| gi ro'oi de poi me [ko'a/ko'e/...] zo'u de me [ko'a/ko'e/...] |
Under these conditions, there is no need that what is x1 of {pa mei} is an individual.
When we use Definitions (D1) (D2) (D3) without using Axiom 1 of Section 3.1, a condition {gi'e su'o pa mei} must be added to {de} of (D1)(When Axiom 1 is used, referents in the domain of variable {de} satisfies this condition automatically).
- Unofficial definitions under the condition that Axiom 1 is abandoned
| (D1') ko'a su'o N mei | =ca'e | su'oi da poi me ko'a ku'o su'oi de poi me ko'a gi'e su'o pa mei zo'u ge da su'o N-1 mei ginai de me da |
| (D2) ko'a N mei | =ca'e | ko'a su'o N mei gi'e nai su'o N+1 mei |
| (D3) lo PA broda | =ca'e | zo'e noi ke'a PA mei gi'e broda |
Using these definitions, inner quantification of what is neither an individual nor individuals becomes possible. Moreover, "Unofficial definition of {piPA} of inner quantification" discussed above becomes able to be applied to what is neither an individual nor individuals.
The diagram below shows a procedure of counting up what is neither an individual nor individuals represented with a directed graph. In this diagram, loops such as {X me X} are omitted for simplicity, though they exist. Among infinite number of vertices (plural constants), the vertices that a speaker selected as {su'o pa mei} are colored pink. Counting up corresponds to selecting a tree that is a subgraph of a directed graph formed with {me}, for example the part of blue color in the diagram.
Outer quantification
BPFK defines outer quantification as follows:
| PA sumti | PA da poi ke'a me sumti | |
| PA broda | PA da poi broda | |
| piPA sumti | lo piPA si'e be pa me sumti | |
Outer quantification except {piPA} forms {PA da}, which is officially a bound singular variable. It implies that these arguments satisfy a predicate distributively. For example, it is meaningless to use {ci lo prenu} as x1 of {jmaji} (gather), because it is not the case that each of three people satisfies the predicate "gather".
However, if we use unofficial plural quantifiers {ro'oi} or {su'oi} for PA, outer quantification can form bound plural variable. For example,
su'oi prenu cu jmaji there are people who gather.
This proposition is implied by a proposition including plural constant
lo prenu cu jmaji People gather.
with the logical axiom in Section 2.2.6.
{PA lo broda} differs from {PA broda} in domain of referents of bound singular variable to be counted. The definitions of outer quantification are applied to them as follows:
| PA lo broda | PA da poi ke'a me lo broda | The domain of bound singular variable is a referent of plural constant {lo broda} in the universe of discourse, and counted to be PA |
| PA broda | PA da poi ke'a broda | The domain of bound singular variable is all that are {broda} in the universe of discourse, and counted to be PA |
- Example 1
- ro jmive ba morsi All living things will die.
- Example 2
- ro lo prenu ti klama All the people come here.
Example 1 mentions all {jmive} in the universe of discourse. In the universe of discourse of Example 2, it is possible to interpret that there are {prenu} other than the referent of the plural constant {lo prenu}.
The outer quantification by {piPA} forms plural constant {lo piPA si'e}. However, x2 of {piPA si'e} is bound singular variable {pa mesumti}. {pi} in this definition means "not larger than 1"; practically, {fi'u} or something can be used instead of {pi}
Combination of outer and inner quantifications
The definitions of inner and outer quantification imply the following interpretations:
| M lo [N] broda | M (which satisfies a predicate distributively) of {lo broda} [that are N] | |
| M loi [N] broda | M (which satisfies a predicate distributively) of {lo gunma} that consists of {lo broda} [that are N] | |
| M lo'i [N] broda | M (which satisfies a predicate distributively) of {lo selcmi} that consists of {lo broda} [that are N] | |
| pi M lo [N] broda | Quantity {pi M si'e} of a part of one of {lo broda} [that are N] | |
| pi M loi [N] broda | Quantity {pi M si'e} of a part of one of {lo gunma} that consists of {lo broda} [that are N] | |
| pi M lo'i [N] broda | Quantity {pi M si'e} of a part (subset) of one of {lo selcmi} that consists of {lo broda} [that are N] | |
Among them, {M lo [N] broda} and {pi M loi [N] broda} can express some of plural number of things.
- Example 1
- re lo [ci] mlatu mi viska Two [of three] cats see me.
- Example 2
- re fi'u ci loi [vei ci pi'i ny (ve'o)] mlatu mi viska Two third of [3n] cats see me.
{re lo [ci] mlatu} of Example 1 refers to two cats among [three] cats that are referent of {lo [ci] mlatu}.
If the inner quantifier {ci} is not said, it is unclear how many cats are referred to by {lo mlatu}; in any case {re lo mlatu} refers to two of them.
In Example 2, the argument is formed by {loi}, and the referent is actually {lo gunma}. Expanding Example 2 according to the definitions of {loi} and {piPA sumti},
- Example 2-1
- lo re fi'u ci si'e be pa me lo gunma be lo [vei ci pi'i ny (ve'o)] mlatu mi viska
That is to say, {re fi'u ci loi...} refers to two third of an individual {pa me lo gunma...}. This {lo gunma} consists of {vei ci pi'i ny (ve'o)} cats. If the inner quantifier is not said, it is unclear how many cats constitute {lo gunma} that is {loi mlatu}; in any case {re fi'u ci loi mlatu} refers to two third of {lo gunma}. However,
re fi'u ci loi mlatu mi viska
is meaningful only when {loi mlatu} consists of 3n cats, because it is not ordinary to interpret that a fragment of a cat satisfies the predicate {viska}. According to BPFK's definition, {loi} cannot form a plural constant that satisfies a predicate non-collectively. If you want to mean "cats see me non-collectively", avoid {loi}, or use {lu'a}, which will be discussed in Section 3.3:
lu'a re fi'u ci loi mlatu mi viska
Bound variables and constants in a statement
When both bound variables and constants appear in a statement, the constants do not necessarily span over all bound variables. Although they are called "constants", it is not generally determined whether they refer to common referents for all referents in domains of variables, or they refer to different referents dependent on referents in domains of variables. The reason follows below (Discussion).
When some sumti of terbri in a statement are omitted, it is considered that there are implicit {zo'e} in those places (CLL 7.7). For example,
ro mlatu cu jbena
All cats are/will be born.
seems to be true from a standard point of view. According to definition of terbri of {jbena}, it is considered that three sumti are omitted, and this statement has the same meaning as
ro mlatu cu jbena zo'e zo'e zo'e
in which {zo'e} are explicit. Unless all cats in this universe of discourse are/will be born to common parents at the same time at the same place, these {zo'e} cannot be considered as common constants for all referents in a domain of {ro mlatu}. In order to make such an expression like {ro mlatu cu jbena} have intended meaning, "constants" of Lojban can be dependent on referents in domains of bound variables.
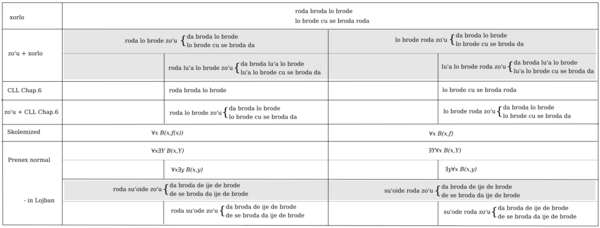
"Constants" in this meaning correspond to Skolem functions in Skolem normal forms of predicate logic. The table below shows comparison of interpretations between predicate logic, xorlo on which this commentary depends and implicit quantifier (CLL Chapter 6) which was abolished. The expressions that have the same truth value are aligned in the same column. Upper case Y represents a plural variable. The row of zo'u+xorlo shows unofficial suggestion of interpretation. In the gray part in the row of Prenex normal, unofficial expressions with an experimental cmavo {su'oi} are shown. (Click on the table to enlarge.)
Relation between lu'a, lu'o, lu'i and gadri
BPFK defines {lu'a}, {lu'o}, {lu'i} of LAhE as follows:
| lu'a sumti | lo me sumti | lo cmima be sumti [noi selcmi] |
| lu'o sumti | loi me sumti | |
| lu'i sumti | lo'i me sumti | |
However, guessing from the English definitions on the same page, the definition of {lu'a} is unsatisfactory, and that of {lu'o} has some problem.
{lu'a} extracts x2 of {selcmi} from sumti that is {lo selcmi}, and x2 of {gunma} from sumti that is {lo gunma}. Moreover, {lu'a} makes explicit that the sumti satisfies a predicate distributively and non-collectively. On the other hand, according to the definition of {lo}, {lo me sumti} does not imply "distributively and non-collectively".
{lu'o} makes explicit that the sumti satisfies a predicate non-distributively and collectively. On the other hand, according to the definition of {loi}, {loi me sumti} satisfies a predicate collectively, but still unclear if it does non-distributively. For consistency, it would be better to add "{loi broda} implies that referent of x1 of broda collectively and non-distributively satisfies a predicate" to the definition of {loi}.
As a conclusion of this section, I suggest to re-define {lu'a} as follows:
- Unofficial definition of {lu'a}
| lu'a sumti | lo cmima be sumti noi selcmi ku onai lo se gunma be sumti noi gunma ku onai lo me sumti ku vu'o noi su'o da zo'u da me ke'a gi'e no'a | |
In {noi} clause after {vu'o}, it is made explicit that the referent of {lu'a sumti} distributively satisfies the sentence that includes this sumti.
Relation between jo'u, joi, ce and gadri
According to BPFK Section, {jo'u}, {joi} and {ce} of selma'o JOI are defined as follows:
| X jo'u Y | lo suzmei noi X .e Y .e no drata be X .e Y cu me ke'a | |
| X joi Y | lo gunma be X .e Y .e no drata be X .e Y | |
| X ce Y | lo se cmima be X .e Y .e no drata be X .e Y | |
They correspond respectively to {lo}, {loi}, {lo'i} of gadri. They connect two sumti: {jo'u} forms a plural constant, {joi} a non-distributive plural constant, {ce} a plural constant that refers to set(s) that consist(s) of the sumti that {ce} connects. In the English definition of {joi} of BPFK, "non-distributive" is mentioned. This fact also supports the suggestion in Section 3.3 to add "{loi broda} implies that referent of x1 of broda collectively and non-distributively satisfies a predicate" to the definition of {loi}.
Even if X or Y are bound variables, these connectives form constants. In this case, it is not determined whether the formed constants depend on X and Y, or they are common to all referents in the domains of X and Y. See Section 3.2.2 for detail.
Because they are cmavo in selma'o JOI, they can connect what are not sumti, but the meanings in this usage are not officially defined. They can form also forethought connective {JOI gi X gi Y}. When the forethought connectives are used for sumti, they form the same constants as the afterthought usage defined above.
Notes
This section consists of notes of the author guskant, and it is not at all important for understanding gadri.
About ontology
Positive impact: Some usages that make little sense with {lo}={su'o} become validated. according to BPFK.
{lo}={su'o} was abandoned, but because of the fact that {lo broda} is a plural constant, and because of a logical axiom of plural constant in Section 2.2.6, {lo broda cu brode} implicitly implies {su'oi da brode}.
claxu x2
le cmana lo cidja ba claxu
In the mountains there is no food.
lapoi pelxu ku'o trajynobli
Expanding {lo cidja},
le cmana zo'e noi ke'a cidja ku'o ba claxu
According to the definition of {noi},
le cmana zo'e to ri xi rau cidja toi ba claxu
The part between {to} and {toi} is a parenthetical expression. The main proposition is thus
le cmana zo'e ba claxu
where {zo'e} is a plural constant. According to the logical axiom of plural constant in Section 2.2.6, This proposition implies
su'oi da zo'u le cmana da ba claxu
which means that there is a referent of "what is lacked by the mountain" in the universe of discourse. The strangeness comes from the fact that x2 of {claxu} apparently means non-existence. We can interpret it consistently that {claxu} means only that the referent of x2 is not placed at the referent of x1, and it says nothing about existence in the universe of discourse.
zo'e is a plural constant
Assuming that {zo'e} can be any of free variable, bound plural variable or plural constant, the language would be more reasonable from a logical point of view. However, this idea was clearly denied in the discussion. That is to say, {zo'e} is always a plural constant according to the official interpretation. I will examine these conflicting ideas, and try to solve some problems caused by the official interpretation that {zo'e} is a plural constant.
If zo'e could be a bound plural variable
I will list up here merits and demerits of assuming that {zo'e} in no context is a free variable, and that the context determines the universe of discourse, based on which {zo'e} is regarded as substituted for by a plural constant, or bound by a plural quantifier.
Merits
Under this assumption, there is no need to exclude the case PA=0 of {lo PA broda}, or give it an unofficial definition as discussed in Section 3.1.2.1. It is because if {lo PA broda} in no context is a free variable, we can interpret it, when a context is given, as substituted for by a plural constant or bound by a plural quantifier like {su'oi da} in the case of PA>0; we can interpret it as bound by {naku su'oi da} in the case of PA=0 as well.
This assumption makes the interpretation closer to natural languages not only in the case PA=0 but also in the case PA>0. For example,
lo ci xanto cu zilkancu li ci lo xanto
The last {lo xanto} is a unit of counting. It is natural to interpret it as a bound plural variable quantified by "1" rather than a plural constant, which should refer to something. If we interpret it as a bound plural variable, we should consider the relative order with the other bound variables and {naku}. We can handle the order freely by putting the arguments in prenex.
Moreover, this assumption embodies the property of natural languages that the truth value of a proposition in no context is generally indefinite. By interpreting that {zo'e} in no context is a free variable, which will be substituted for by a plural constant or bound by a plural quantifier when a context is given, natural interpretation of Lojban sentence is possible without losing logical aspects and structural beauty.
Demerits
Because {zo'e} can be a free variable, a bound plural variable or a plural constant depending on the context, a single bridi does not let listeners determine which of them is the current {zo'e}, or the truth value of the proposition. However, such an aspect that the truth value of a proposition generally depends on the context is a common property to all natural languages.
On the other hand, even if we take the official interpretation that {zo'e} is always a plural constant, listeners are only informed by {zo'e} that a certain universe of discourse is given. With no context, there is no way to determine what is the universe of discourse. The truth value of a proposition in no context is indefinite even with the official interpretation.
Problems caused by the fact that zo'e is a plural constant and the counter-measures
The official interpretation that {zo'e} is a plural constant causes the following problems.
Cannot express plural quantification of non-existence
Reasonable interpretation of {lo no broda} is officially excluded from Lojban. That is to say, Lojban cannot officially deal with the expression "there is not what is substituted for {da}" for plural variable ({naku su'oi da}), which is naturally dealt with by plural quantification. In order to express {lo no broda} with reasonable interpretation, we need an unofficial interpretation like Section 3.1.2.1.
Cannot express bound plural variable, which does not specify a referent
Because the official interpretation does not allow {lo PA broda} to be a bound plural variable depending on the context, an argument that should refer to nothing, a unit of counting for example, should be interpreted as a plural constant, which refers to something. For example
lo ci xanto cu zilkancu li ci lo xanto
for which we are compelled to interpret that there is the "Elephant des Archives" in the universe of discourse, just like the "Mètre des Archives" (although it has already finished its role), in order to use {lo xanto} as a unit in a proposition.
Cannot express elementary particles with lo
As long as {lo broda} is interpreted as a plural constant, the following Lojban sentence is meaningless:
lo guska'u cu gau jmaji sepi'o lo lenjo gi'e pagre lo fenra
Photons are condensed by lenses, and pass through slits.
Actually, photons are individuals, and we can count them, but we cannot distinguish each of them: we cannot refer to a specific photon. Quantification is indeed suitable for arguments that represent particles like photons. However, Lojban officially does not have a plural quantifier, and cannot express quantification of sumti that satisfies selbri both collectively and distributively. Moreover, because {lo broda} is officially always a plural constant, there is no room to interpret {lo guska'u} as a bound plural variable. In order to solve the problem, we should use an unofficial plural quantifier {su'oi} suggested by la xorxes.
su'oi da poi ke'a guska'u cu gau jmaji sepi'o lo lenjo gi'e pagre lo fenra
How to interpret a prevailing view
The following example is given on BPFK's gadri page:
lo pa pixra cu se vamji lo ki'o valsi
One picture is worth a thousand words.
Even in such a sentence that seems a prevailing view, {lo pa pixra} and {lo ki'o valsi} are interpreted as referring to something. We should prepare some referents of sumti of a prevailing view in the universe of discourse.
Intuitionally speaking, we may use {lo'e} instead of {lo}, but we cannot yet explain {lo'e} from a logical point of view because actually there is no official conclusion about relation between {lo'e} and {lo}.
As a method of avoiding mention of a referent in an expression of prevailing view, we may put the whole proposition in NU clause. In fact, truth value of a proposition in NU clause does not influence truth value of the outer proposition (referentially opaque; this topic is related to CLL9.7). In other words, the universe of discourse of a proposition in NU clause is different from the universe of discourse of a proposition out of NU. If we accept this method, the example above will be modified, using {si'o} for example, as follows:
si'o lo pa pixra cu se vamji lo ki'o valsi
Is an idea that one picture is worth a thousand words.
where x1 of {si'o} is implicit {zo'e}, which has a referent in the universe of discourse. As an interpretation of a prevailing view, supposing a referent of x1 of {si'o} is more natural than supposing a referent of {lo pa pixra} or {lo ki'o valsi}.
(Such a bridi with no terbri is called "observative" in the Complete Lojban Language, but this interpretation is not suitable here, because this is not the utterance that is always caused by a specific stimulus.)
How to express free variables
As a custom, ko'V/fo'V series of KOhA4 are used as free variables in definitions of words or something. However, they are actually plural constants. If we abandon this custom, {ke'a} and {ce'u} are suitable for expression with free variables (open sentence), because the truth value of bridi in which {ke'a} or {ce'u} is used is indefinite. In a bridi in which {ke'a} appears two times or more, these {ke'a}s are regarded as representing an identical sumti:
da poi ke'a gy xlura ke'a cu panci lo ka'e se citka
— lo nu binxo
On the other hand, in a bridi in which {ce'u} appears two times or more, these {ce'u}s are not necessarily regarded as representing an identical sumti:
lo mamta jo'u lo mensi cu simxu lo ka ce'u cisma fa'a ce'u
— lo nu binxo
Considering these properties, in order to express an open sentence with free variables in no context, {ce'u} is more convenient than {ke'a} which has restriction of identical sumti.
ce'u ce'u citka
A eats B. (Open sentence, truth value indefinite.)