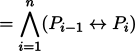zantufa jonma'o smuni/fr

banjubu'o / français / 日本語 / English

Sémantique de conjonctions prépositives logiques

Les conjonctions prépositives de la zantufa qui est une série d'analyseurs du lojban officieux sont beaucoup plus expressives que celles de la grammaire officielle.

La zantufa est un analyseur syntactique, qui ne fixe pas de règle de la sémantique par elle-même.

Voici simplement une suggestion de la sémantique de conjonctions prépositives logiques pour qu'on profite de l'expressivité de la grammaire de la zantufa.

Les phrases suivantes en lojban observent la grammaire de la zantufa_1.16.

Liste de symboles apparaissants sur cette page

Symbole	Définition
¬P	na ku P
P ∨ Q	P i ja Q
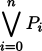
	((((P0 ∨ P1) ∨ P2) ∨ ...) ∨ Pn)
P ∧ Q	P i je Q
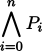
	((((P0 ∧ P1) ∧ P2) ∧ ...) ∧ Pn)
P ↔ Q	P i jo Q
	((((P0 ↔ P1) ↔ P2) ↔ ...) ↔ Pn)
P ⊕ Q	P i jonai Q
	((((P0 ⊕ P1) ⊕ P2) ⊕ ...) ⊕ Pn)
P ⊏ Q	P i ju Q
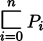
	((((P0 ⊏ P1) ⊏ P2) ⊏ ...) ⊏ Pn) = P0
P ⊐ Q	P i se ju Q
	((((P0 ⊐ P1) ⊐ P2) ⊐ ...) ⊐ Pn) = Pn

Dans l'explication suivante, des exemples de la conjonction 3-aire ou 4-aire sont parfois accompagnés d'un tableau de valeur de vérité. Le faux est signifie d'un chiffre 0; le vrai est signifie d'un chiffre 1.

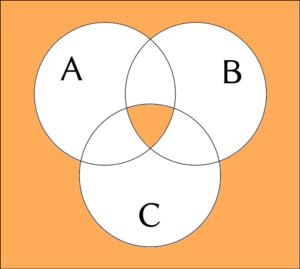
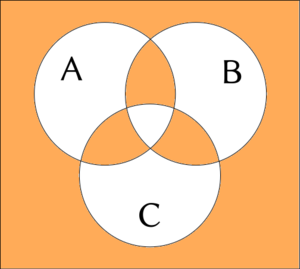
Des exemples de la conjonction 3-aire sont parfois accompagnés d'un diagramme Venn. La couleur blanche signifie le faux; la couleur orange signifie le vrai.

ga

ga A gi B gi C gi ...

Définition

ga P0 gi P1 gi ... gi Pn (gi'i)

=

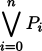
Exemple

Le cas 3-aire: {ga A gi B gi C}=(A∨B)∨C

ga zei ven

A	B	C	A∨B	(A∨B)∨C
1	1	1	1	1
0	1	1	1	1
1	0	1	1	1
0	0	1	0	1
1	1	0	1	1
0	1	0	1	1
1	0	0	1	1
0	0	0	0	0

ga bo A gi B gi C gi ...

Définition

	ga bo P0 gi P1 gi ... gi Pn (gi'i)
=	ga P0 gi P1 gi ... gi Pn (gi'i)
=

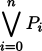
ga nai A gi B gi C gi ...

Définition

	ga nai P0 gi P1 gi ... gi Pn (gi'i)
=	ga ¬P0 gi P1 gi ... gi Pn (gi'i)

Exemple

Le cas 3-aire: {ga nai A gi B gi C}=(¬A∨B)∨C

ga zei nai zei ven

A	B	C	¬A∨B	(¬A∨B)∨C
1	1	1	1	1
0	1	1	1	1
1	0	1	0	1
0	0	1	1	1
1	1	0	1	1
0	1	0	1	1
1	0	0	0	0
0	0	0	1	1

ga nai bo A gi B gi C gi ...

Définition

ga nai bo P0 gi P1 gi ... gi Pn (gi'i)

Exemple

Le cas 3-aire:

	{ga nai bo A gi B gi C}
=	((A→B)∧(B→C))
=	((¬A∨B)∧(¬B∨C))

ga zei nai zei bo zei ven

A	B	C	¬A∨B	¬B∨C	(¬A∨B)∧(¬B∨C)
1	1	1	1	1	1
0	1	1	1	1	1
1	0	1	0	1	0
0	0	1	1	1	1
1	1	0	1	0	0
0	1	0	1	0	0
1	0	0	0	1	0
0	0	0	1	1	1

Différence

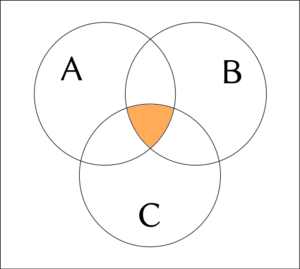
{ga nai bo A gi B gi C} ≠ {A i na ja B i na ja C}

	A i na ja B i na ja C
=	(A → B) → C
=	¬(¬A ∨ B) ∨ C

i zei na zei ja zei ven

A	B	C	¬A∨B	¬(¬A∨B)∨C
1	1	1	1	1
0	1	1	1	1
1	0	1	0	1
0	0	1	1	1
1	1	0	1	0
0	1	0	1	0
1	0	0	0	1
0	0	0	1	0

ge

ge A gi B gi C gi ...

Définition

	ge P0 gi P1 gi ... gi Pn (gi'i)
=

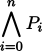
Exemple

Le cas 3-aire: {ge A gi B gi C}=(A∧B)∧C

ge zei ven

A	B	C	A∧B	(A∧B)∧C
1	1	1	1	1
0	1	1	0	0
1	0	1	0	0
0	0	1	0	0
1	1	0	1	0
0	1	0	0	0
1	0	0	0	0
0	0	0	0	0

ge bo A gi B gi C gi ...

Définition

	ge bo P0 gi P1 gi ... gi Pn (gi'i)
=	ge P0 gi P1 gi ... gi Pn (gi'i)
=

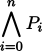
ge nai A gi B gi C gi ...

Définition

	ge nai P0 gi P1 gi ... gi Pn (gi'i)
=	ge ¬P0 gi P1 gi ... gi Pn (gi'i)

Exemple

Le cas 3-aire: {ge nai A gi B gi C}=(¬A∧B)∧C

ge zei nai zei ven

A	B	C	¬A∧B	(¬A∧B)∧C
1	1	1	0	0
0	1	1	1	1
1	0	1	0	0
0	0	1	0	0
1	1	0	0	0
0	1	0	1	0
1	0	0	0	0
0	0	0	0	0

ge nai bo A gi B gi C gi ...

Définition

ge nai bo P0 gi P1 gi ... gi Pn (gi'i)

Exemple

Le cas 3-aire:

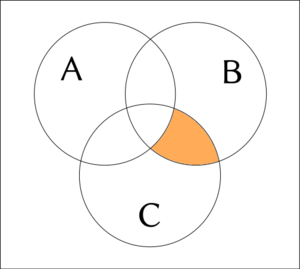
	{ge nai bo A gi B gi C}
=	{ge nai A gi nai B gi nai C}
=	{A i na je nai B i je nai C}
=	(¬A∧¬B)∧¬C

ge zei nai zei bo zei ven

A	B	C	¬A∧¬B	(¬A∧¬B)∧¬C
1	1	1	0	0
0	1	1	0	0
1	0	1	0	0
0	0	1	1	0
1	1	0	0	0
0	1	0	0	0
1	0	0	0	0
0	0	0	1	1

go

go A gi B gi C gi ...

Définition

	go P0 gi P1 gi ... gi Pn (gi'i)
=

Exemple

Le cas 3-aire: {go A gi B gi C}=(A↔B)↔C

go zei ven

A	B	C	A↔B	(A↔B)↔C
1	1	1	1	1
0	1	1	0	0
1	0	1	0	0
0	0	1	1	1
1	1	0	1	0
0	1	0	0	1
1	0	0	0	1
0	0	0	1	0

go bo A gi B gi C gi ...

Définition

go bo P0 gi P1 gi ... gi Pn (gi'i)

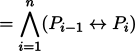
Exemple

Le cas 3-aire:

	{go bo A gi B gi C}
=	((A↔B)∧(B↔C))

go zei bo zei ven

A	B	C	A↔B	B↔C	(A↔B)∧(B↔C)
1	1	1	1	1	1
0	1	1	0	1	0
1	0	1	0	0	0
0	0	1	1		0
1	1	0	1	0	0
0	1	0	0	0	0
1	0	0	0	1	0
0	0	0	1	1	1

go nai A gi B gi C gi ...

Définition

	go nai P0 gi P1 gi ... gi Pn (gi'i)
=	go ¬P0 gi P1 gi ... gi Pn (gi'i)

Exemple

Le cas 3-aire: {go nai A gi B gi C}=(¬A↔B)↔C

go zei nai zei ven

A	B	C	¬A↔B	(¬A↔B)↔C
1	1	1	0	0
0	1	1	1	1
1	0	1	1	1
0	0	1	0	0
1	1	0	0	1
0	1	0	1	0
1	0	0	1	0
0	0	0	0	1

go nai bo A gi B gi C gi ...

Définition

C'est définie récursivement comme suit.

Le cas 2-aire de P₀ et P₁:

	go nai bo P0 gi P1 (gi'i)
=	go nai P0 gi P1 (gi'i)
=	P0 ⊕ P1
=	¬P0 ↔ P1

Le cas 3-aire de P₀, ... , P_n (n≥2):

	go nai bo P0 gi ... gi Pn (gi'i)
=	((go nai bo P0 gi ... gi Pn-1 (gi'i)) ⊕ Pn) ∧

Exemple

Le cas 3-aire:

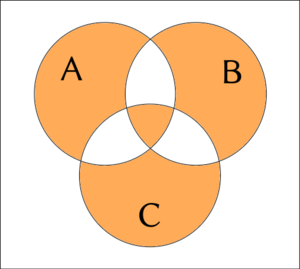
	{go nai bo A gi B gi C}
=	((go nai A gi B) ⊕ C) ∧ ¬(A∧B)
=	((A⊕B)⊕C) ∧ ¬(A∧B)

go zei nai zei bo zei ven

A	B	C	A⊕B	(A⊕B)⊕C	¬(A∧B)	((A⊕B)⊕C) ∧ ¬(A∧B)
1	1	1	0	1	0	0
0	1	1	1	0	1	0
1	0	1	1	0	1	0
0	0	1	0	1	1	1
1	1	0	0	0	0	0
0	1	0	1	1	1	1
1	0	0	1	1	1	1
0	0	0	0	0	1	0

Le cas 4-aire:

	{go nai bo A gi B gi C gi D}
=	((go nai bo A gi B gi C) ⊕ D) ∧ ¬(A∧B) ∧ ¬(B∧C) ∧ ¬(C∧A)

A	B	C	D	go nai bo A gi B gi C	(go nai bo A gi B gi C) ⊕ D	¬(A∧B)	¬(B∧C)	¬(C∧A)	((go nai bo A gi B gi C) ⊕ D) ∧ ¬(A∧B) ∧ ¬(B∧C) ∧ ¬(C∧A)
1	1	1	1	0	1	0	0	0	0
0	1	1	1	0	1	1	0	1	0
1	0	1	1	0	1	1	1	0	0
0	0	1	1	1	0	1	1	1	0
1	1	0	1	0	1	0	1	1	0
0	1	0	1	1	0	1	1	1	0
1	0	0	1	1	0	1	1	1	0
0	0	0	1	0	1	1	1	1	1
1	1	1	0	0	0	0	0	0	0
0	1	1	0	0	0	1	0	1	0
1	0	1	0	0	0	1	1	0	0
0	0	1	0	1	1	1	1	1	1
1	1	0	0	0	0	0	1	1	0
0	1	0	0	1	1	1	1	1	1
1	0	0	0	1	1	1	1	1	1
0	0	0	0	0	0	1	1	1	0

Différence

{go nai bo P₀ gi P₁ gi ... gi P_n (gi'i)} ≠ {P₀ i jo nai P₁ i jo nai ... i jo nai P_n}

Voici, par exemple, le tableau de valeur de vérité de la conjonction jusqu'à 4-aire par {i jo nai}, qui est différent de celui de {go nai bo A gi B gi C gi D}.

	{A i jo nai B i jo nai C i jo nai D}
=	{A i na jo B i na jo C i na jo D}
=	((A ⊕ B) ⊕ C) ⊕ D

i zei jo zei nai zei ven

A	B	C	D	A ⊕ B	(A ⊕ B) ⊕ C	((A ⊕ B) ⊕ C) ⊕ D
1	1	1	1	0	1	0
0	1	1	1	1	0	1
1	0	1	1	1	0	1
0	0	1	1	0	1	0
1	1	0	1	0	0	1
0	1	0	1	1	1	0
1	0	0	1	1	1	0
0	0	0	1	0	0	1
1	1	1	0	0	1	1
0	1	1	0	1	0	0
1	0	1	0	1	0	0
0	0	1	0	0	1	1
1	1	0	0	0	0	0
0	1	0	0	1	1	1
1	0	0	0	1	1	1
0	0	0	0	0	0	0

gu

gu A gi B gi C gi ...

Définition

	gu P0 gi P1 gi ... gi Pn (gi'i)
=
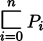
=	P0

Exemple

Le cas 3-aire:

	{gu A gi B gi C}
=	(A ⊏ B) ⊏ C
=	A

gu zei ven

gu bo A gi B gi C gi ...

Définition

	gu bo P0 gi P1 gi ... gi Pn (gi'i)
=	gu P0 gi P1 gi ... gi Pn (gi'i)
=
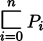
=	P0

gu nai A gi B gi C gi ...

Définition

	gu nai P0 gi P1 gi ... gi Pn (gi'i)
=	gu ¬P0 gi P1 gi ... gi Pn (gi'i)
=	¬P0

Exemple

Le cas 3-aire:

	{gu nai A gi B gi C}
=	{gu ¬A gi B gi C}
=	¬A

gu zei nai zei ven

gu nai bo A gi B gi C gi ...

Définition

	gu nai bo P0 gi P1 gi ... gi Pn (gi'i)
	gu ¬P0 gi ¬P1 gi ... gi ¬Pn (gi'i)
=	¬P0
=	gu nai P0 gi P1 gi ... gi Pn (gi'i)

segu

se xi ky gu A gi B gi C gi ... (se gu, te gu, ve gu, xe gu, ..., se xi ro gu)

	se xi ky gu P0 gi P1 gi ... gi Pn (gi'i)
=	P0 i se ju P1 i se ju ... i se ju Pk i ju ... i ju Pn
=	i ju ... i ju Pn
=	Pk i ju ... i ju Pn
=
=	Pk

{se xi no gu}	=	{gu}
{se xi pa gu}	=	{se gu}
{se xi re gu}	=	{te gu}
{se xi ci gu}	=	{ve gu}
{se xi vo gu}	=	{xe gu}
	...

{se xi ro gu P0 gi P1 gi ... gi Pn (gi'i)}

=

Pn

se xi ky gu bo A gi B gi C gi ...

	se xi ky gu bo P0 gi P1 gi ... gi Pn (gi'i)
=	se xi ky gu P0 gi P1 gi ... gi Pn (gi'i)
=	Pk

se xi ky gu nai A gi B gi C gi ...

Au cas où k=0

	se xi no gu nai P0 gi P1 gi ... gi Pn (gi'i)
=	gu ¬P0 gi P1 gi ... gi Pn (gi'i)
=	¬P0

Au cas où k≠0

	se xi ky gu nai P0 gi P1 gi ... gi Pn (gi'i)
=	se xi ky gu ¬P0 gi P1 gi ... gi Pn (gi'i)
=	Pk

se xi ky gu nai bo A gi B gi C gi ...

	se xi ky gu nai bo P0 gi P1 gi ... gi Pn (gi'i)
=	se xi ky gu ¬P0 gi ¬P1 gi ... gi ¬Pk gi ... gi ¬Pn (gi'i)
=	¬Pk