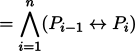前置型論理接続詞の意味論
非公式のロジバン構文解析器 zantufa の前置型接続は、公式文法に比べて非常に豊かな表現力を持つ。
zantufa 自体は構文解析器であり意味論を規定しないが、 zantufa 文法の豊かな表現力を有効に活用するものとして、以下のような前置型論理接続詞の意味論を提案する。
以下のロジバン文は zantufa_1.16 の文法に従う。
このページで使われる記号のリスト
| 記号
|
意味
|
| ¬P
|
na ku P
|
| P ∨ Q
|
P i ja Q
|
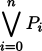
|
((((P0 ∨ P1) ∨ P2) ∨ ...) ∨ Pn)
|
| P ∧ Q
|
P i je Q
|
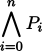
|
((((P0 ∧ P1) ∧ P2) ∧ ...) ∧ Pn)
|
| P ↔ Q
|
P i jo Q
|

|
((((P0 ↔ P1) ↔ P2) ↔ ...) ↔ Pn)
|
| P ⊕ Q
|
P i jonai Q
|

|
((((P0 ⊕ P1) ⊕ P2) ⊕ ...) ⊕ Pn)
|
| P ⊏ Q
|
P i ju Q
|
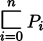
|
((((P0 ⊏ P1) ⊏ P2) ⊏ ...) ⊏ Pn)
= P0
|
| P ⊐ Q
|
P i se ju Q
|

|
((((P0 ⊐ P1) ⊐ P2) ⊐ ...) ⊐ Pn)
= Pn
|
以下の説明中、3項や4項の接続例について真理値表を与えることがある。 偽を 0、 真を 1 で表す。
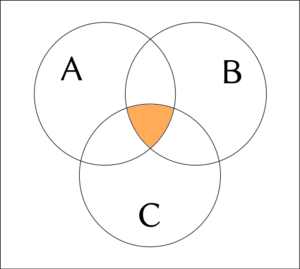
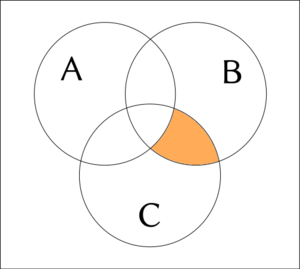
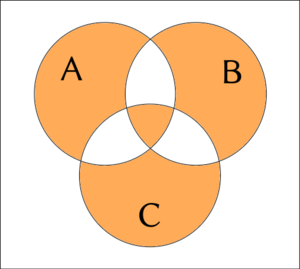
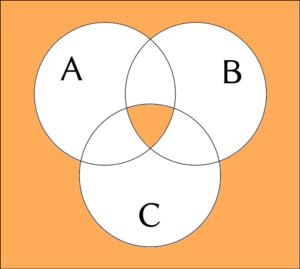
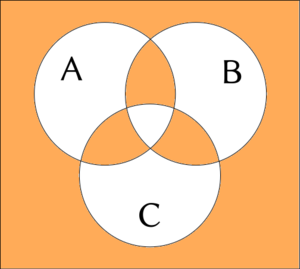
3項の接続例について Venn 図を与えることがある。 白色は偽、オレンジ色は真を表す。
ga
ga A gi B gi C gi ...
定義
| ga P0 gi P1 gi ... gi Pn (gi'i)
|
= 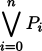
|
例
3項の場合: {ga A gi B gi C}=(A∨B)∨C
| A
|
B
|
C
|
A∨B
|
(A∨B)∨C
|
| 1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
1
|
1
|
1
|
| 0
|
0
|
1
|
0
|
1
|
| 1
|
1
|
0
|
1
|
1
|
| 0
|
1
|
0
|
1
|
1
|
| 1
|
0
|
0
|
1
|
1
|
| 0
|
0
|
0
|
0
|
0
|
ga bo A gi B gi C gi ...
定義
|
|
ga bo P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
ga P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
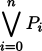
|
ga nai A gi B gi C gi ...
定義
|
|
ga nai P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
ga ¬P0 gi P1 gi ... gi Pn (gi'i)
|
例
3項の場合: {ga nai A gi B gi C}=(¬A∨B)∨C
| A
|
B
|
C
|
¬A∨B
|
(¬A∨B)∨C
|
| 1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
1
|
0
|
1
|
| 0
|
0
|
1
|
1
|
1
|
| 1
|
1
|
0
|
1
|
1
|
| 0
|
1
|
0
|
1
|
1
|
| 1
|
0
|
0
|
0
|
0
|
| 0
|
0
|
0
|
1
|
1
|
ga nai bo A gi B gi C gi ...
定義
| ga nai bo P0 gi P1 gi ... gi Pn (gi'i)
|

|
例
3項の場合:
|
|
{ga nai bo A gi B gi C}
|
| =
|
((A→B)∧(B→C))
|
| =
|
((¬A∨B)∧(¬B∨C))
|

ga zei nai zei bo zei ven
| A
|
B
|
C
|
¬A∨B
|
¬B∨C
|
(¬A∨B)∧(¬B∨C)
|
| 1
|
1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
1
|
1
|
1
|
| 1
|
0
|
1
|
0
|
1
|
0
|
| 0
|
0
|
1
|
1
|
1
|
1
|
| 1
|
1
|
0
|
1
|
0
|
0
|
| 0
|
1
|
0
|
1
|
0
|
0
|
| 1
|
0
|
0
|
0
|
1
|
0
|
| 0
|
0
|
0
|
1
|
1
|
1
|
相違点
{ga nai bo A gi B gi C} ≠ {A i na ja B i na ja C}
|
|
A i na ja B i na ja C
|
| =
|
(A → B) → C
|
| =
|
¬(¬A ∨ B) ∨ C
|
| A
|
B
|
C
|
¬A∨B
|
¬(¬A∨B)∨C
|
| 1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
1
|
0
|
1
|
| 0
|
0
|
1
|
1
|
1
|
| 1
|
1
|
0
|
1
|
0
|
| 0
|
1
|
0
|
1
|
0
|
| 1
|
0
|
0
|
0
|
1
|
| 0
|
0
|
0
|
1
|
0
|
ge
ge A gi B gi C gi ...
定義
|
|
ge P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
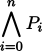
|
例
3項の場合: {ge A gi B gi C}=(A∧B)∧C
| A
|
B
|
C
|
A∧B
|
(A∧B)∧C
|
| 1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
0
|
0
|
| 1
|
0
|
1
|
0
|
0
|
| 0
|
0
|
1
|
0
|
0
|
| 1
|
1
|
0
|
1
|
0
|
| 0
|
1
|
0
|
0
|
0
|
| 1
|
0
|
0
|
0
|
0
|
| 0
|
0
|
0
|
0
|
0
|
ge bo A gi B gi C gi ...
定義
|
|
ge bo P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
ge P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
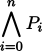
|
ge nai A gi B gi C gi ...
定義
|
|
ge nai P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
ge ¬P0 gi P1 gi ... gi Pn (gi'i)
|
例
3項の場合: {ge nai A gi B gi C}=(¬A∧B)∧C
| A
|
B
|
C
|
¬A∧B
|
(¬A∧B)∧C
|
| 1
|
1
|
1
|
0
|
0
|
| 0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
1
|
0
|
0
|
| 0
|
0
|
1
|
0
|
0
|
| 1
|
1
|
0
|
0
|
0
|
| 0
|
1
|
0
|
1
|
0
|
| 1
|
0
|
0
|
0
|
0
|
| 0
|
0
|
0
|
0
|
0
|
ge nai bo A gi B gi C gi ...
定義
| ge nai bo P0 gi P1 gi ... gi Pn (gi'i)
|

|
例
3項の場合:
|
|
{ge nai bo A gi B gi C}
|
| =
|
{ge nai A gi nai B gi nai C}
|
| =
|
{A i na je nai B i je nai C}
|
| =
|
(¬A∧¬B)∧¬C
|

ge zei nai zei bo zei ven
| A
|
B
|
C
|
¬A∧¬B
|
(¬A∧¬B)∧¬C
|
| 1
|
1
|
1
|
0
|
0
|
| 0
|
1
|
1
|
0
|
0
|
| 1
|
0
|
1
|
0
|
0
|
| 0
|
0
|
1
|
1
|
0
|
| 1
|
1
|
0
|
0
|
0
|
| 0
|
1
|
0
|
0
|
0
|
| 1
|
0
|
0
|
0
|
0
|
| 0
|
0
|
0
|
1
|
1
|
go
go A gi B gi C gi ...
定義
|
|
go P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|

|
例
3項の場合: {go A gi B gi C}=(A↔B)↔C
| A
|
B
|
C
|
A↔B
|
(A↔B)↔C
|
| 1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
0
|
0
|
| 1
|
0
|
1
|
0
|
0
|
| 0
|
0
|
1
|
1
|
1
|
| 1
|
1
|
0
|
1
|
0
|
| 0
|
1
|
0
|
0
|
1
|
| 1
|
0
|
0
|
0
|
1
|
| 0
|
0
|
0
|
1
|
0
|
go bo A gi B gi C gi ...
定義
| go bo P0 gi P1 gi ... gi Pn (gi'i)
|
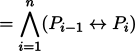
|
例
3項の場合:
|
|
{go bo A gi B gi C}
|
| =
|
((A↔B)∧(B↔C))
|
| A
|
B
|
C
|
A↔B
|
B↔C
|
(A↔B)∧(B↔C)
|
| 1
|
1
|
1
|
1
|
1
|
1
|
| 0
|
1
|
1
|
0
|
1
|
0
|
| 1
|
0
|
1
|
0
|
0
|
0
|
| 0
|
0
|
1
|
1
|
|
0
|
| 1
|
1
|
0
|
1
|
0
|
0
|
| 0
|
1
|
0
|
0
|
0
|
0
|
| 1
|
0
|
0
|
0
|
1
|
0
|
| 0
|
0
|
0
|
1
|
1
|
1
|
go nai A gi B gi C gi ...
定義
|
|
go nai P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
go ¬P0 gi P1 gi ... gi Pn (gi'i)
|
例
3項の場合: {go nai A gi B gi C}=(¬A↔B)↔C
| A
|
B
|
C
|
¬A↔B
|
(¬A↔B)↔C
|
| 1
|
1
|
1
|
0
|
0
|
| 0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
1
|
1
|
1
|
| 0
|
0
|
1
|
0
|
0
|
| 1
|
1
|
0
|
0
|
1
|
| 0
|
1
|
0
|
1
|
0
|
| 1
|
0
|
0
|
1
|
0
|
| 0
|
0
|
0
|
0
|
1
|
go nai bo A gi B gi C gi ...
定義
以下のように再帰的に定義される。
2項 P0, P1 の場合:
|
|
go nai bo P0 gi P1 (gi'i)
|
| =
|
go nai P0 gi P1 (gi'i)
|
| =
|
P0 ⊕ P1
|
| =
|
¬P0 ↔ P1
|
3項以上 P0, ... , Pn (n≥2) の場合:
|
|
go nai bo P0 gi ... gi Pn (gi'i)
|
| =
|
((go nai bo P0 gi ... gi Pn-1 (gi'i)) ⊕ Pn) ∧ 
|
例
3項の場合:
|
|
{go nai bo A gi B gi C}
|
| =
|
((go nai A gi B) ⊕ C) ∧ ¬(A∧B)
|
| =
|
((A⊕B)⊕C) ∧ ¬(A∧B)
|

go zei nai zei bo zei ven
| A
|
B
|
C
|
A⊕B
|
(A⊕B)⊕C
|
¬(A∧B)
|
((A⊕B)⊕C) ∧ ¬(A∧B)
|
| 1
|
1
|
1
|
0
|
1
|
0
|
0
|
| 0
|
1
|
1
|
1
|
0
|
1
|
0
|
| 1
|
0
|
1
|
1
|
0
|
1
|
0
|
| 0
|
0
|
1
|
0
|
1
|
1
|
1
|
| 1
|
1
|
0
|
0
|
0
|
0
|
0
|
| 0
|
1
|
0
|
1
|
1
|
1
|
1
|
| 1
|
0
|
0
|
1
|
1
|
1
|
1
|
| 0
|
0
|
0
|
0
|
0
|
1
|
0
|
4項の場合:
|
|
{go nai bo A gi B gi C gi D}
|
| =
|
((go nai bo A gi B gi C) ⊕ D) ∧ ¬(A∧B) ∧ ¬(B∧C) ∧ ¬(C∧A)
|
| A
|
B
|
C
|
D
|
go nai bo A gi B gi C
|
(go nai bo A gi B gi C) ⊕ D
|
¬(A∧B)
|
¬(B∧C)
|
¬(C∧A)
|
((go nai bo A gi B gi C) ⊕ D) ∧ ¬(A∧B) ∧ ¬(B∧C) ∧ ¬(C∧A)
|
| 1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
| 0
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
| 1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
| 0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
| 1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
| 0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
| 1
|
0
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
| 0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
| 1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
| 1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
| 0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
| 1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
| 0
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
| 1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
| 0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
相違点
{go nai bo P0 gi P1 gi ... gi Pn (gi'i)} ≠ {P0 i jo nai P1 i jo nai ... i jo nai Pn}
例えば4項まで {i jo nai} で接続すると真理値表は以下のようになり、 {go nai bo A gi B gi C gi D} と異なる。
|
|
{A i jo nai B i jo nai C i jo nai D}
|
| =
|
{A i na jo B i na jo C i na jo D}
|
| =
|
((A ⊕ B) ⊕ C) ⊕ D
|
| A
|
B
|
C
|
D
|
A ⊕ B
|
(A ⊕ B) ⊕ C
|
((A ⊕ B) ⊕ C) ⊕ D
|
| 1
|
1
|
1
|
1
|
0
|
1
|
0
|
| 0
|
1
|
1
|
1
|
1
|
0
|
1
|
| 1
|
0
|
1
|
1
|
1
|
0
|
1
|
| 0
|
0
|
1
|
1
|
0
|
1
|
0
|
| 1
|
1
|
0
|
1
|
0
|
0
|
1
|
| 0
|
1
|
0
|
1
|
1
|
1
|
0
|
| 1
|
0
|
0
|
1
|
1
|
1
|
0
|
| 0
|
0
|
0
|
1
|
0
|
0
|
1
|
| 1
|
1
|
1
|
0
|
0
|
1
|
1
|
| 0
|
1
|
1
|
0
|
1
|
0
|
0
|
| 1
|
0
|
1
|
0
|
1
|
0
|
0
|
| 0
|
0
|
1
|
0
|
0
|
1
|
1
|
| 1
|
1
|
0
|
0
|
0
|
0
|
0
|
| 0
|
1
|
0
|
0
|
1
|
1
|
1
|
| 1
|
0
|
0
|
0
|
1
|
1
|
1
|
| 0
|
0
|
0
|
0
|
0
|
0
|
0
|
gu
gu A gi B gi C gi ...
定義
|
|
gu P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
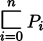
|
| =
|
P0
|
例
3項の場合:
|
|
{gu A gi B gi C}
|
| =
|
(A ⊏ B) ⊏ C
|
| =
|
A
|
gu bo A gi B gi C gi ...
定義
|
|
gu bo P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
gu P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
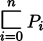
|
| =
|
P0
|
gu nai A gi B gi C gi ...
定義
|
|
gu nai P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
gu ¬P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
¬P0
|
例
3項の場合:
|
|
{gu nai A gi B gi C}
|
| =
|
{gu ¬A gi B gi C}
|
| =
|
¬A
|
gu nai bo A gi B gi C gi ...
定義
|
|
gu nai bo P0 gi P1 gi ... gi Pn (gi'i)
|
|
|
gu ¬P0 gi ¬P1 gi ... gi ¬Pn (gi'i)
|
| =
|
¬P0
|
| =
|
gu nai P0 gi P1 gi ... gi Pn (gi'i)
|
segu
se xi ky gu A gi B gi C gi ... (se gu, te gu, ve gu, xe gu, ..., se xi ro gu)
|
|
se xi ky gu P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
P0 i se ju P1 i se ju ... i se ju Pk i ju ... i ju Pn
|
| =
|
 i ju ... i ju Pn i ju ... i ju Pn
|
| =
|
Pk i ju ... i ju Pn
|
| =
|

|
| =
|
Pk
|
| {se xi no gu}
|
=
|
{gu}
|
| {se xi pa gu}
|
=
|
{se gu}
|
| {se xi re gu}
|
=
|
{te gu}
|
| {se xi ci gu}
|
=
|
{ve gu}
|
| {se xi vo gu}
|
=
|
{xe gu}
|
|
|
...
|
|
| {se xi ro gu P0 gi P1 gi ... gi Pn (gi'i)}
|
=
|
Pn
|
se xi ky gu bo A gi B gi C gi ...
|
|
se xi ky gu bo P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
se xi ky gu P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
Pk
|
se xi ky gu nai A gi B gi C gi ...
k=0 のとき
|
|
se xi no gu nai P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
gu ¬P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
¬P0
|
k≠0 のとき
|
|
se xi ky gu nai P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
se xi ky gu ¬P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
Pk
|
se xi ky gu nai bo A gi B gi C gi ...
|
|
se xi ky gu nai bo P0 gi P1 gi ... gi Pn (gi'i)
|
| =
|
se xi ky gu ¬P0 gi ¬P1 gi ... gi ¬Pk gi ... gi ¬Pn (gi'i)
|
| =
|
¬Pk
|